It started with a mysterious soft lockup message in production. A single, cryptic line that led us down a rabbit hole into the performance of one of the most fundamental data structures we use: the BPF LPM trie.
BPF trie maps (BPF_MAP_TYPE_LPM_TRIE) are heavily used for things like IP and IP+Port matching when routing network packets, ensuring your request passes through the right services before returning a result. The performance of this data structure is critical for serving our customers, but the speed of the current implementation leaves a lot to be desired. We’ve run into several bottlenecks when storing millions of entries in BPF LPM trie maps, such as entry lookup times taking hundreds of milliseconds to complete and freeing maps locking up a CPU for over 10 seconds. For instance, BPF maps are used when evaluating Cloudflare’s Magic Firewall rules and these bottlenecks have even led to traffic packet loss for some customers.
This post gives a refresher of how tries and prefix matching work, benchmark results, and a list of the shortcomings of the current BPF LPM trie implementation.
If it’s been a while since you last looked at the trie data structure (or if you’ve never seen it before), a trie is a tree data structure (similar to a binary tree) that allows you to store and search for data for a given key and where each node stores some number of key bits.
Searches are performed by traversing a path, which essentially reconstructs the key from the traversal path, meaning nodes do not need to store their full key. This differs from a traditional binary search tree (BST) where the primary invariant is that the left child node has a key that is less than the current node and the right child has a key that is greater. BSTs require that each node store the full key so that a comparison can be made at each search step.
Here’s an example that shows how a BST might store values for the keys:
-
ABC
-
ABCD
-
ABCDEFGH
-
DEF

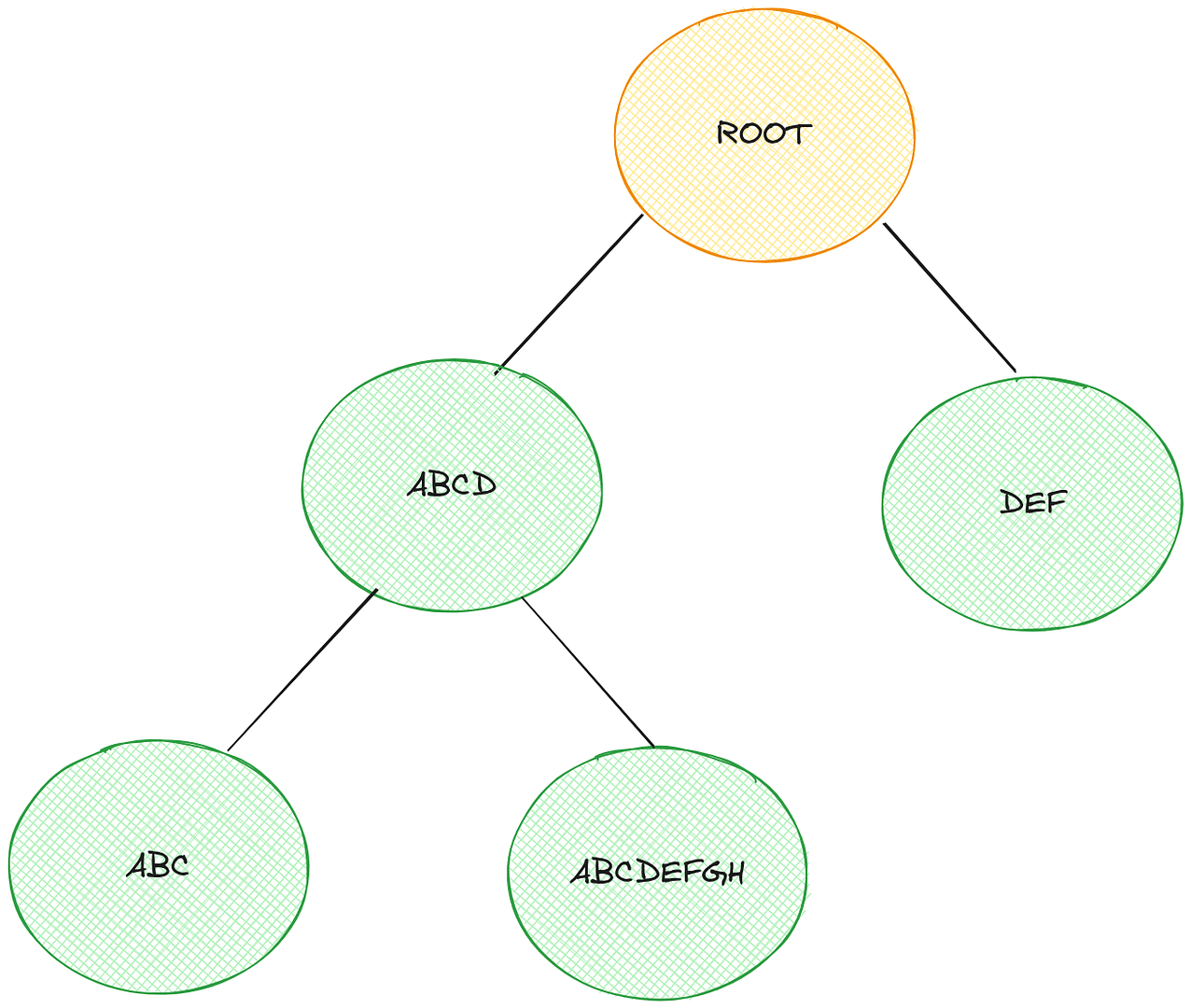
In comparison, a trie for storing the same set of keys might look like this.

This way of splitting out bits is really memory-efficient when you have redundancy in your data, e.g. prefixes are common in your keys, because that shared data only requires a single set of nodes. It’s for this reason that tries are often used to efficiently store strings, e.g. dictionaries of words – storing the strings “ABC” and “ABCD” doesn’t require 3 bytes + 4 bytes (assuming ASCII), it only requires 3 bytes + 1 byte because “ABC” is shared by both (the exact number of bits required in the trie is implementation dependent).
Tries also allow more efficient searching. For instance, if you wanted to know whether the key “CAR” existed in the BST you are required to go to the right child of the root (the node with key “DEF”) and check its left child because this is where it would live if it existed. A trie is more efficient because it searches in prefix order. In this particular example, a trie knows at the root whether that key is in the trie or not.
This design makes tries perfectly suited for performing longest prefix matches and for working with IP routing using CIDR. CIDR was introduced to make more efficient use of the IP address space (no longer requiring that classes fall into 4 buckets of 8 bits) but comes with added complexity because now the network portion of an IP address can fall anywhere. Handling the CIDR scheme in IP routing tables requires matching on the longest (most specific) prefix in the table rather than performing a search for an exact match.
If searching a trie does a single-bit comparison at each node, that’s a binary trie. If searching compares more bits we call that a multibit trie. You can store anything you like in a trie, including IP and subnet addresses – it’s all just ones and zeroes.
Nodes in multibit tries use more memory than in binary tries, but since computers operate on multibit words anyhow, it’s more efficient from a microarchitecture perspective to use multibit tries because you can traverse through the bits faster, reducing the number of comparisons you need to make to search for your data. It’s a classic space vs time tradeoff.
There are other optimisations we can use with tries. The distribution of data that you store in a trie might not be uniform and there could be sparsely populated areas. For example, if you store the strings “A” and “BCDEFGHI” in a multibit trie, how many nodes do you expect to use? If you’re using ASCII, you could construct the binary trie with a root node and branch left for “A” or right for “B”. With 8-bit nodes, you’d need another 7 nodes to store “C”, “D”, “E”, “F”, “G”, “H”, “I”.

Since there are no other strings in the trie, that’s pretty suboptimal. Once you hit the first level after matching on “B” you know there’s only one string in the trie with that prefix, and you can avoid creating all the other nodes by using path compression. Path compression replaces nodes “C”, “D”, “E” etc. with a single one such as “I”.

If you traverse the tree and hit “I”, you still need to compare the search key with the bits you skipped (“CDEFGH”) to make sure your search key matches the string. Exactly how and where you store the skipped bits is implementation dependent – BPF LPM tries simply store the entire key in the leaf node. As your data becomes denser, path compression is less effective.
What if your data distribution is dense and, say, all the first 3 levels in a trie are fully populated? In that case you can use level compression and replace all the nodes in those levels with a single node that has 2**3 children. This is how Level-Compressed Tries work which are used for IP route lookup in the Linux kernel (see net/ipv4/fib_trie.c).
There are other optimisations too, but this brief detour is sufficient for this post because the BPF LPM trie implementation in the kernel doesn’t fully use the three we just discussed.
Here are some numbers from running BPF selftests benchmark on AMD EPYC 9684X 96-Core machines. Here the trie has 10K entries, a 32-bit prefix length, and an entry for every key in the range [0, 10K).
|
Operation |
Throughput |
Stddev |
Latency |
|
lookup |
7.423M ops/s |
0.023M ops/s |
134.710 ns/op |
|
update |
2.643M ops/s |
0.015M ops/s |
378.310 ns/op |
|
delete |
0.712M ops/s |
0.008M ops/s |
1405.152 ns/op |
|
free |
0.573K ops/s |
0.574K ops/s |
1.743 ms/op |
The time to free a BPF LPM trie with 10K entries is noticeably large. We recently ran into an issue where this took so long that it caused soft lockup messages to spew in production.
This benchmark gives some idea of worst case behaviour. Since the keys are so densely populated, path compression is completely ineffective. In the next section, we explore the lookup operation to understand the bottlenecks involved.
The LPM trie implementation in kernel/bpf/lpm_trie.c has a couple of the optimisations we discussed in the introduction. It is capable of multibit comparisons at leaf nodes, but since there are only two child pointers in each internal node, if your tree is densely populated with a lot of data that only differs by one bit, these multibit comparisons degrade into single bit comparisons.
Here’s an example. Suppose you store the numbers 0, 1, and 3 in a BPF LPM trie. You might hope that since these values fit in a single 32 or 64-bit machine word, you could use a single comparison to decide which next node to visit in the trie. But that’s only possible if your trie implementation has 3 child pointers in the current node (which, to be fair, most trie implementations do). In other words, you want to make a 3-way branching decision but since BPF LPM tries only have two children, you’re limited to a 2-way branch.
A diagram for this 2-child trie is given below.

The leaf nodes are shown in green with the key, as a binary string, in the center. Even though a single 8-bit comparison is more than capable of figuring out which node has that key, the BPF LPM trie implementation resorts to inserting intermediate nodes (blue) to inject 2-way branching decisions into your path traversal because its parent (the orange root node in this case) only has 2 children. Once you reach a leaf node, BPF LPM tries can perform a multibit comparison to check the key. If a node supported pointers to more children, the above trie could instead look like this, allowing a 3-way branch and reducing the lookup time.

This 2-child design impacts the height of the trie. In the worst case, a completely full trie essentially becomes a binary search tree with height log2(nr_entries) and the height of the trie impacts how many comparisons are required to search for a key.
The above trie also shows how BPF LPM tries implement a form of path compression – you only need to insert an intermediate node where you have two nodes whose keys differ by a single bit. If instead of 3, you insert a key of 15 (0b1111), this won’t change the layout of the trie; you still only need a single node at the right child of the root.

And finally, BPF LPM tries do not implement level compression. Again, this stems from the fact that nodes in the trie can only have 2 children. IP route tables tend to have many prefixes in common and you typically see densely packed tries at the upper levels which makes level compression very effective for tries containing IP routes.
Here’s a graph showing how the lookup throughput for LPM tries (measured in million ops/sec) degrades as the number of entries increases, from 1 entry up to 100K entries.

Once you reach 1 million entries, throughput is around 1.5 million ops/sec, and continues to fall as the number of entries increases.

Why is this? Initially, this is because of the L1 dcache miss rate. All of those nodes that need to be traversed in the trie are potential cache miss opportunities.

As you can see from the graph, L1 dcache miss rate remains relatively steady and yet the throughput continues to decline. At around 80K entries, dTLB miss rate becomes the bottleneck.

Because BPF LPM tries to dynamically allocate individual nodes from a freelist of kernel memory, these nodes can live at arbitrary addresses. Which means traversing a path through a trie almost certainly will incur cache misses and potentially dTLB misses. This gets worse as the number of entries, and height of the trie, increases.

By understanding the current limitations of the BPF LPM trie, we can now work towards building a more performant and efficient solution for the future of the Internet.
We’ve already contributed these benchmarks to the upstream Linux kernel — but that’s only the start. We have plans to improve the performance of BPM LPM tries, particularly the lookup function which is heavily used for our workloads. This post covered a number of optimisations that are already used by the net/ipv4/fib_trie.c code, so a natural first step is to refactor that code so that a common Level Compressed trie implementation can be used. Expect future blog posts to explore this work in depth.
If you’re interested in looking at more performance numbers, Jesper Brouer has recorded some here: https://github.com/xdp-project/xdp-project/blob/main/areas/bench/bench02_lpm-trie-lookup.org.